As notações assintóticas não falam diretamente sobre algoritmos, mas sim sobre funções. Mais especificamente, sobre funções que levam números naturais em números reais.

Definição 1.1 (notação \(O\)). Sejam \(f\) e \(g\) duas funções de \(\mathbb{N}\) em \(\mathbb{R}\). Dizemos que \(f\) é \(O(g)\) quando existe um número real \(c > 0\) e um \(n_0 \in \mathbb{N}\) tais que, para todo número natural \(n \geq n_0\), \(f(n) \leq c \cdot g(n)\).

Para quem já estudou Cálculo/Análise Real, vai perceber que essa definição lembra um pouco a definição de limite de sequência. A ideia é que, a partir de um número natural \(n_0\) suficientemente grande, a função \(f\) fica abaixo de um múltiplo de \(g\). Desse modo, podemos pensar que \(g\) atua como um limite superior para o comportamento assintótico da função \(f\).

As notações \(\Omega\) e \(\Theta\) são definidas de forma similar:

Definição 1.2 (notação \(\Omega\)). Sejam \(f, g: \mathbb{N} \to \mathbb{R}\). Dizemos que \(f\) é \(\Omega(g)\) quando existe um número real \(c > 0\) e um \(n_0 \in \mathbb{N}\) tais que, para todo número natural \(n \geq n_0\), \(c \cdot g(n) \leq f(n)\).

Podemos pensar em \(\Omega\) como o conceito dual a \(O\): enquanto \(O\) descreve um limite superior para o comportamento assintótico de uma função, \(\Omega\) descreve um limite inferior.

Definição 1.3 (notação \(\Theta\)). Sejam \(f, g: \mathbb{N} \to \mathbb{R}\). Dizemos que \(f\) é \(\Omega(g)\) quando existem números reais \(c_1, c_2 > 0\) e um \(n_0 \in \mathbb{N}\) tais que, para todo número natural \(n \geq n_0\), \(c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)\).

Podemos pensar em \(\Theta\) como uma junção das notações \(O\) e \(\Omega\). De fato, é possível provar que \(f\) é \(\Theta(g)\) se, e somente se, \(f\) é \(O(g)\) e \(f\) é \(\Omega(g)\).

As explicações da seção anterior passam a ideia de que podemos ordenar as funções com base em seu comportamento assintótico. Isso de fato é possível, e meu objetivo nesta seção é mostrar como construímos esta ordem.

Primeiro, começamos definindo o conjunto de funções que vamos analisar. Iremos denotar por \(\mathcal{F}\) o conjunto de todas as funções de \(\mathbb{N}\) em \(\mathbb{R}\).

Definição 2.1. Sejam \(f, g \in \mathcal{F}\). Dizemos que \(f\) é assintoticamente menor ou igual que \(g\), denotado por \(f \preceq g\), quando existe um número real \(c > 0\) e um \(n_0 \in \mathbb{N}\) tais que, para todo número natural \(n \geq n_0\), \(f(n) \leq c \cdot g(n)\).

Essa definição é idêntica à definição da notação \(O\). Assim, dizer que \(f \preceq g\) é o mesmo que dizer que \(f\) é \(O(g)\). De fato, se pensamos em \(g\) como um limite superior assintótico para \(f\), temos que, assintoticamente, \(f\) está abaixo de \(g\).

Proposição 2.2. Sejam \(f, g, h \in \mathcal{F}\). Valem as seguintes propriedades:

1. \(f \preceq f\);
2. se \(f \preceq g\) e \(g \preceq h\), então \(f \preceq h\);
3. \(f \preceq g\) se, e somente se, existe um número real \(c > 0\) e um \(n_0 \in \mathbb{N}\) tais que, para todo número natural \(n \geq n_0\), \(c \cdot f(n) \leq g(n)\).

Prova. Fica como exercício para o leitor. \(\blacksquare\)

O item 3 da proposição acima nos diz que \(f \preceq g\) se, e somente se, \(g\) é \(\Omega(f)\). Daí, segue também uma propriedade curiosa da notação assintótica: \(f\) é \(O(g)\) se, e somente se, \(g\) é \(\Omega(f)\). Pensando em termos de limites (superior e inferior), essa propriedade é bem intuitiva: se \(g\) é um limite superior de \(f\), \(f\) vai ser um limite inferior de \(g\), e vice-versa. Quando utilizamos uma notação como \(\preceq\), essa simetria/dualidade fica clara.

Os itens 1 e 2 da proposição acima mostram que \(\preceq\) é uma pré-ordem. A partir de uma pré-ordem, podemos definir uma relação de equivalência.

Definição 2.3. Sejam \(f, g \in \mathcal{F}\). Dizemos que \(f\) é assintoticamente equivalente a g, denotado por \(f \sim g\), quando \(f \preceq g\) e \(g \preceq f\).

Se \(\preceq\) fosse uma relação de ordem, a relação de equivalência assintótica, definida acima, seria simplesmente a igualdade. Porém, podemos ter funções diferentes que são assintoticamente equivalentes.

Exemplo 2.4. Sejam \(f, g: \mathbb{N} \to \mathbb{R}\) as funções definidas por \(f(n) = n\) e \(g(n) = \dfrac{n}{2}\). Note que, para todo \(n \in \mathbb{N}\): \[f(n) = n \leq n = 2 \cdot \dfrac{n}{2} = 2 \cdot g(n)\] \[g(n) = \dfrac{n}{2} \leq \dfrac{n}{2} = \dfrac{1}{2} \cdot n = \dfrac{1}{2} \cdot f(n)\]

Logo, \(f \preceq g\) e \(g \preceq f\). Ou seja, \(f \sim g\), mas \(f \neq g\).

Proposição 2.5. Sejam \(f, g \in \mathcal{F}\). Então, \(f \sim g\) se, e somente se, \(f\) é \(\Theta(g)\).

Prova.

\((\Rightarrow)\) Suponha que \(f \sim g\). Como \(g \preceq f\), pelo item 3 da proposição anterior, existem \(c_1 > 0\) e \(n_1 \in \mathbb{N}\) tais que, para todo \(n \geq n_1\), \(c_1 \cdot g(n) \leq f(n)\).

Além disso, como \(f \preceq g\), existem \(c_2 > 0\) e \(n_2 \in \mathbb{N}\) tais que, para todo \(n \geq n_2\), \(f(n) \leq c_2 \cdot g(n)\).

Assim, considere \(n_0 = \max \{n_1, n_2\}\). Temos que, para todo \(n \geq n_0\), \(c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)\). Logo, \(f\) é \(\Theta(g)\).

\((\Leftarrow)\) Suponha que \(f\) é \(\Theta(g)\). Sabemos que existem \(c_1, c_2 > 0\) e \(n_0 \in \mathbb{N}\) tais que, para todo \(n \geq n_0\), \(c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)\). Em particular, vale que \(g \preceq f\) e \(f \preceq g\), ou seja, \(f \sim g\). \(\blacksquare\)

A proposição acima conecta a notação \(\Theta\) com a nova linguagem apresentada nessa seção. Quando duas funções são assintoticamente equivalentes, podemos pensar que elas tem o mesmo comportamento assintótico. E é isso que nos permite fazer certas simplificações quando encontramos funções mais complexas dentro de um \(O\), por exemplo.

Proposição 2.6. Sejam \(f, g \in \mathcal{F}\) e \(\alpha \in \mathbb{R}\) tais que \(0 \preceq f\) e \(\alpha > 0\). Valem as seguintes propriedades:

1. se \(f \preceq g\), então \(f + g \sim g\);
2. \(f \sim \alpha \cdot f\).

Prova. Para o item 1, suponha que \(f \preceq g\). Como \(0 \preceq f\), pelo item 3 da Proposição 2.3, temos que existem \(c_1 > 0\) e \(n_1 \in \mathbb{N}\) tais que, para todo \(n \geq n_1\), \(c_1 \cdot 0 \leq f(n)\), ou seja, \(0 \leq f(n)\). Daí, \(g(n) \leq f(n) + g(n)\).

Além disso, como \(f \preceq g\), existem \(c_2 > 0\) e \(n_2 \in \mathbb{N}\) tais que, para todo \(n \geq n_2\), \(f(n) \leq c_2 g(n)\). Desse modo, \(f(n) + g(n) \leq c_2 g(n) + g(n)\), ou seja, \(f(n) + g(n) \leq (c_2 + 1) g(n)\).

Assim, seja \(n_0 = \max\{n_1, n_2\}\). Para todo \(n \geq n_0\), \(g(n) \leq f(n) + g(n) \leq (c_2 + 1) g(n)\). Logo, \(f + g\) é \(\Theta(g)\) e, pela Proposição 2.5, \(f + g \sim g\).

Para o item 2, repetimos o argumento inicial para o item 1: como \(0 \preceq f\), existe \(n_0 \in \mathbb{N}\) tal que, para todo \(n \geq n_0\), \(0 \leq f(n)\). Além disso, temos duas possibilidades para \(\alpha\):

• \(\alpha \geq 1\). Neste caso, considere \(n \geq n_0\). Como \(0 \leq f(n)\), \(f(n) \leq \alpha f(n)\) e \(\dfrac{1}{\alpha} \cdot f(n) \leq f(n)\). Daí, temos que: \[\dfrac{1}{\alpha^2} \cdot \alpha f(n) = \dfrac{1}{\alpha} \cdot f(n) \leq f(n) \leq \alpha f(n)\] Logo, \(f\) é \(\Theta(\alpha f)\) e, pela Proposição 2.5, \(f \sim \alpha f\).
• \(0 < \alpha < 1\). Este caso é análogo ao item anterior e fica como exercício para o leitor.

Assim, \(f \sim \alpha f\). \(\blacksquare\)

A proposição acima é o que justifica ignorarmos constantes e termos de "menor grau" (assintoticamente menores) na notação assintótica. Note que a hipótese \(0 \preceq f\) sempre é satisfeita quando estamos analisando algoritmos: \(f\) retorna o número de passos executados pelo algoritmo, e esse número de passos nunca vai ser negativo.

Uma das principais aplicações da notação assintótica é na análise da complexidade computacional de algoritmos. A complexidade computacional descreve o comportamento assintótico do algoritmo e pode ser feita em duas dimensões: tempo e espaço. Nesta seção, vou explicar como fazemos a análise da complexidade de tempo (a complexidade de espaço pode ser feita de forma similar).

Quando analisamos a complexidade (de tempo) de um algoritmo, queremos entender como o tempo de execução varia em função do tamanho da entrada. Assim, considere \(A\) um algoritmo qualquer, e \(\mathcal{E}(A)\) o conjunto de todas as entradas possíveis para \(A\). O "tamanho da entrada" pode ser descrito como uma função \(s_A: \mathcal{E}(A) \to \mathbb{N}\), que associa a cada entrada em \(\mathcal{E}(A)\) um número natural que descreve o seu tamanho. Também podemos descrever o "tempo de execução" de \(A\) como uma função \(t_A: \mathcal{E}(A) \to \mathbb{R}\) que associa a cada entrada em \(\mathcal{E}(A)\) o número de passos executados pelo algoritmo com essa entrada.

Em geral, não conseguimos conectar as duas funções \(s_A\) e \(t_A\), pois \(s_A\) não é inversível (entradas diferentes podem ter o mesmo tamanho). Mas, para cada tamanho \(n\), podemos analisar o comportamento do algoritmo no conjunto \(s_A^{-1}(n) = \{e \in \mathcal{E}(A) : s_A(e) = n\}\) de todas as entradas de tamanho \(n\). Podemos analisar o pior caso, o melhor caso, o caso médio, etc. Assim, conseguimos associar a cada \(n \in \mathbb{N}\) um tempo de execução, e a partir daí utilizar a notação assintótica para descrever o comportamento do algoritmo, no caso analisado.

Mas como exatamente isso é feito? Para entender melhor, vamos analisar o seguinte algoritmo:

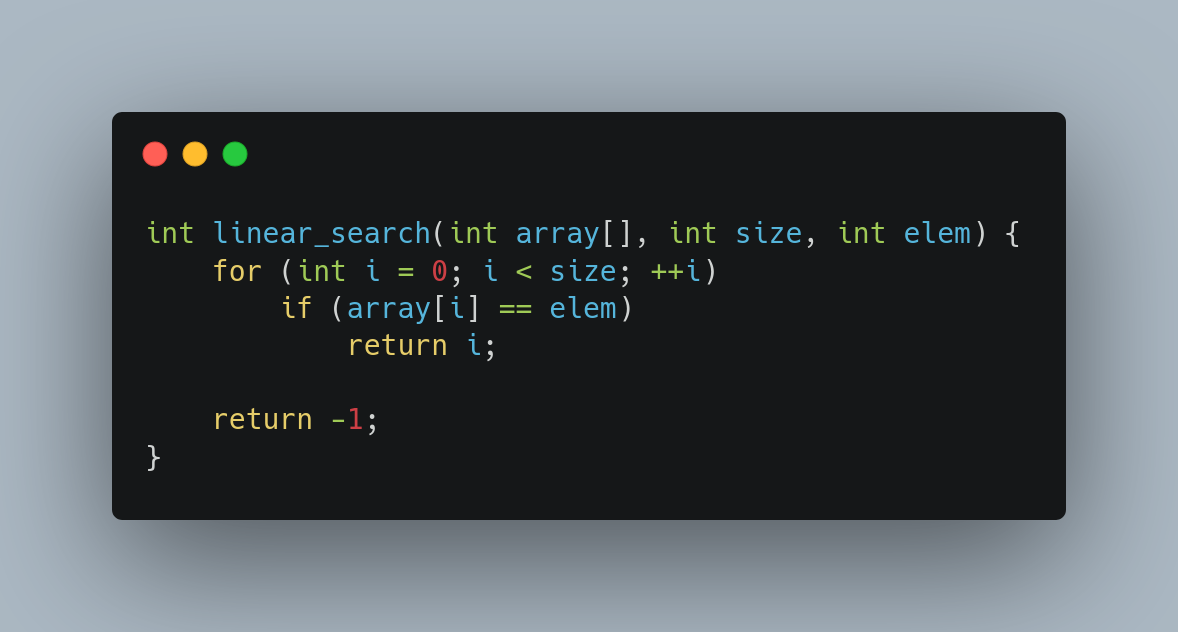
O algoritmo acima, escrito em C, é o de busca linear. Ele percorre o array chamado array de tamanho size até encontrar o elemento elem. Se encontra, retorna a posição do elemento. Caso contrário, retorna -1.

A entrada de linear_search é composta por três argumentos: um array de inteiros e dois números inteiros. Como os números inteiros tem tamanho fixo, podemos descrever o tamanho da entrada como o tamanho do array.

Assim, seja \(n \in \mathbb{N}^*\) e considere um array \(a\) de tamanho \(n\). Se considerarmos que \(a\) cai no melhor caso do algoritmo, significa que o elemento buscado está na posição \(0\) de \(a\), e o loop é executado apenas uma vez. Considerando que o algoritmo realiza apenas três operações (a saber, atribuir o valor \(0\) à variável i, comparar array[i] com elem e retornar i), podemos descrever o número de passos executados pela função: \[m(n) = 3\]

Agora, considere que \(a\) cai no pior caso do algoritmo. Esse caso pode ser obtido selecionando um array que não contém elem. Inicialmente, o valor \(0\) é atribuído à variável i. Para cada iteração (de \(0\) até \(n - 1\)), são executados os seguintes passos:

• a comparação entre array[i] e elem;
• o incremento ++i;
• a comparação i < size.

Ao sair do loop, após a última iteração, ainda é executada mais uma operação: retorna o valor \(-1\). Assim, podemos descrever o número de passos executados pela função: \[p(n) = 1 + 3n + 1 = 3n + 2\]

Agora, tendo a descrição do número de passos executados para o melhor e o pior caso, podemos descrevê-los através da notação assintótica: o pior caso é \(\Theta(1)\) e o melhor caso é \(\Theta(n)\) (como vimos, podemos ignorar constantes e termos de "menor grau").

E o caso geral? Tendo descrito o pior caso, sabemos que todos os outros casos vão estar abaixo dele. Ou seja, se para cada \(n\) selecionamos um array de inteiros qualquer de tamanho \(n\), e descrevemos o número de passos executados pelo algoritmo com essa entrada por \(f(n)\), teremos sempre que \(f \preceq p \preceq n\), ou seja, \(f\) é \(O(n)\). Assim, o algoritmo linear_search é \(O(n)\) (e, de forma análoga, \(\Omega(1)\)).

[1] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest e Clifford Stein. Algoritmos: teoria e prática, quarta edição.

[2] Thomas H. Cormen. Desmistificando algoritmos.

[3] Jayme Luiz Szwarcfiter e Lilian Markenzon. Estruturas de dados e seus algoritmos, terceira edição.